▸ Advice for Applying Machine Learning :
Recommended Machine Learning Courses:
- Coursera: Machine Learning
- Coursera: Deep Learning Specialization
- Coursera: Machine Learning with Python
- Coursera: Advanced Machine Learning Specialization
- Udemy: Machine Learning
- LinkedIn: Machine Learning
- Eduonix: Machine Learning
- edX: Machine Learning
- Fast.ai: Introduction to Machine Learning for Coders
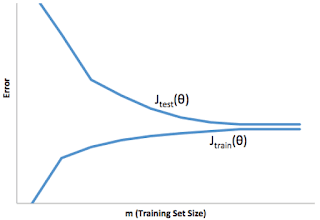
- You train a learning algorithm, and find that it has unacceptably high error on the test set. You plot the learning curve, and obtain the figure below. Is the algorithm suffering from high bias, high variance, or neither?
- You train a learning algorithm, and find that it has unacceptably high error on the test set. You plot the learning curve, and obtain the figure below. Is the algorithm suffering from high bias, high variance, or neither?
- High variance
This learning curve shows high error on the test sets but comparatively low error on training set, so the algorithm is suffering from high variance.
- Neither
- High bias
- High variance
- Suppose you have implemented regularized logistic regression to classify what object is in an image (i.e., to do object recognition). However, when you test your hypothesis on a new set of images, you find that it makes unacceptably large errors with its predictions on the new images. However, your hypothesis performs well (has low error) on the training set. Which of the following are promising steps to take? Check all that apply.
NOTE: Since the hypothesis performs well (has low error) on the training set, it is suffering from high variance (overfitting)
- Try adding polynomial features.
Adding polynomial feature will increase the high variance problem.
- Use fewer training examples.
Decreasing training examples will increase the high variance problem.
- Try using a smaller set of features.
The gap in errors between training and test suggests a high variance problem in which the algorithm has overfit the training set. Reducing the feature set will ameliorate the overfitting and help with the variance problem
- Get more training examples.
The gap in errors between training and test suggests a high variance problem in which the algorithm has overfit the training set. Adding more training data will increase the complexity of the training set and help with the variance problem.
- Try evaluating the hypothesis on a cross validation set rather than the test set.
A cross validation set is useful for choosing the optimal non-model parameters like the regularization parameter λ, but the train / test split is sufficient for debugging problems with the algorithm itself.
- Try decreasing the regularization parameter λ.
The gap in errors between training and test suggests a high variance problem in which the algorithm has overfit the training set. Decreasing the regularization parameter will increase the overfitting, not decrease it.
- Try increasing the regularization parameter λ.
The gap in errors between training and test suggests a high variance problem in which the algorithm has overfit the training set. Increasing the regularization parameter will reduce overfitting and help with the variance problem.
- Try adding polynomial features.
- Suppose you have implemented regularized logistic regression to predict what items customers will purchase on a web shopping site. However, when you test your hypothesis on a new set of customers, you find that it makes unacceptably large errors in its predictions. Furthermore, the hypothesis performs poorly on the training set. Which of the following might be promising steps to take? Check all that apply.
NOTE: Since the hypothesis performs poorly on the training set, it is suffering from high bias (underfitting)
- Try increasing the regularization parameter λ.
The poor performance on both the training and test sets suggests a high bias problem. Increasing the regularization parameter will allow the hypothesis to fit the data worse, decreasing both training and test set performance.
- Try decreasing the regularization parameter λ.
Decreasing the regularization parameter will improve the high bias problem and may improve the performance on the training set.
- Try evaluating the hypothesis on a cross validation set rather than the test set.
You should not use the cross validation set to evaluate performance on new examples since we have used cross validation set to set the regularization parameter, as you will then have an artificially low value for test error and it will not give a good estimate of generalization error.
- Use fewer training examples.
Using fewer training example will make the situation worse. It will not solve the high bias problem but might increase high variance problem as well.
- Try adding polynomial features.
The poor performance on both the training and test sets suggests a high bias problem. Adding more complex features will increase the complexity of the hypothesis, thereby improving the fit to both the train and test data.
- Try using a smaller set of features.
The poor performance on both the training and test sets suggests a high bias problem. Using fewer features will decrease the complexity of the hypothesis and will make the bias problem worse
- Try to obtain and use additional features.
The poor performance on both the training and test sets suggests a high bias problem. Using additional features will increase the complexity of the hypothesis, thereby improving the fit to both the train and test data.
- Try increasing the regularization parameter λ.
- Which of the following statements are true? Check all that apply.
- Suppose you are training a regularized linear regression model. The recommended way to choose what value of regularization parameter to use is to choose the value of which gives the lowest test set error.
You should not use the test set to choose the regularization parameter, as you will then have an artificially low value for test error and it will not give a good estimate of generalization error.
- Suppose you are training a regularized linear regression model.The recommended way to choose what value of regularization parameter to use is to choose the value of which gives the lowest training set error.
You should not use training error to choose the regularization parameter, as you can always improve training error by using less regularization (a smaller value of ). But too small of a value will not generalize well onthe test set.
- The performance of a learning algorithm on the training set will typically be better than its performance on the test set.
The learning algorithm finds parameters to minimize training set error, so the performance should be better on the training set than the test set.
- Suppose you are training a regularized linear regression model. The recommended way to choose what value of regularization parameter to use is to choose the value of which gives the lowest cross validation error.
The cross validation lets us find the “just right” setting of the regularization parameter given the fixed model parameters learned from the training set.
- A typical split of a dataset into training, validation and test sets might be 60% training set, 20% validation set, and 20% test set.
This is a good split of the data, as it dedicates the bulk of the data to finding model parameters in training while leaving enough data for cross validation and estimating generalization error.
- Suppose you are training a logistic regression classifier using polynomial features and want to select what degree polynomial (denoted in the lecture videos) to use. After training the classifier on the entire training set, you decide to use a subset of the training examples as a validation set. This will work just as well as having a validation set that is separate (disjoint) from the training set.
cross validation set should not be the subset of training set. Training / Cross validation / Test set should be similar (from same source) but disjoint.
- It is okay to use data from the test set to choose the regularization parameter λ, but not the model parameters (θ).
We should not use test set data to choose any of the parameters (regularization and model parameters)
- Suppose you are using linear regression to predict housing prices, and your dataset comes sorted in order of increasing sizes of houses. It is then important to randomly shuffle the dataset before splitting it into training, validation and test sets, so that we don’t have all the smallest houses going into the training set, and all the largest houses going into the test set.
We should shuffle the data before spliting it into training / cross validation / test set.
- Suppose you are training a regularized linear regression model. The recommended way to choose what value of regularization parameter to use is to choose the value of which gives the lowest test set error.
Check-out our free tutorials on IOT (Internet of Things):
- Which of the following statements are true? Check all that apply.
- A model with more parameters is more prone to overfitting and typically has higher variance.
More model parameters increases the model’s complexity, so it can more tightly fit data in training, increasing the chances of overfitting.
- If the training and test errors are about the same, adding more features will not help improve the results.
Training and test errors are about the same means model is facing high bias problem. Adding more features will help in solving high bias problem.
- If a learning algorithm is suffering from high bias, only adding more training examples may not improve the test error significantly.
For solving high bias problem, adding more features useful but adding more training example won’t help.
- If a learning algorithm is suffering from high variance, adding more training examples is likely to improve the test error.
Adding more training data solves the high variance problem.
- When debugging learning algorithms, it is useful to plot a learning curve to understand if there is a high bias or high variance problem.
The shape of a learning curve is a good indicator of bias or variance problems with your learning algorithm.
- If a neural network has much lower training error than test error, then adding more layers will help bring the test error down because we can fit the test set better.
With lower training than test error, the model has high variance. Adding more layers will increase model complexity, making the variance problem worse.
- A model with more parameters is more prone to overfitting and typically has higher variance.
Click here to see solutions for all Machine Learning Coursera Assignments.
&
Click here to see more codes for Raspberry Pi 3 and similar Family.
&
Click here to see more codes for NodeMCU ESP8266 and similar Family.
&
Click here to see more codes for Arduino Mega (ATMega 2560) and similar Family.
Feel free to ask doubts in the comment section. I will try my best to answer it.
If you find this helpful by any mean like, comment and share the post.
This is the simplest way to encourage me to keep doing such work.
&
Click here to see more codes for Raspberry Pi 3 and similar Family.
&
Click here to see more codes for NodeMCU ESP8266 and similar Family.
&
Click here to see more codes for Arduino Mega (ATMega 2560) and similar Family.
Feel free to ask doubts in the comment section. I will try my best to answer it.
If you find this helpful by any mean like, comment and share the post.
This is the simplest way to encourage me to keep doing such work.
Thanks & Regards,
- APDaga DumpBox
- APDaga DumpBox